As someone who has studied radioactivity in detail, I have always been a bit amused by the assertion that radioactive dating is a precise way to determine the age of an object. This false notion is often promoted when radioactive dates are listed with utterly unrealistic error bars. In this report, for example, we are told that using one radioactive dating technique, a lunar rock sample is 4,283 million years old, plus or minus 23 million years old. In other words, there is a 95% certainty that the age is somewhere between 4,283 + 23 million years and 4,283 – 23 million years. That’s just over half a percent error in something that is supposedly multiple billions of years old.
Of course, that error estimate is complete nonsense. It refers to one specific source of error – the uncertainty in the measurement of the amounts of various atoms used in the analysis. Most likely, that is the least important source of error. If those rocks really have been sitting around on the moon for billions of years, I suspect that the the wide range of physical and chemical processes which occurred over that time period had a much more profound effect on the uncertainty of the age determination. This is best illustrated by the radioactive age of a sample of diamonds from Zaire. Their age was measured to be 6.0 +/- 0.3 billion years old. Do you see the problem? Those who are committed to an ancient age for the earth currently believe that it is 4.6 billion years old. Obviously, then, the minimum error in that measurement is 1.4 billion years, not 0.3 billion years!
Such uncertainties are usually glossed over, especially when radioactive dates are communicated to the public and, more importantly, to students. Generally, we are told that scientists have ways to analyze the object they are dating so as to eliminate the uncertainties due to unknown processes that occurred in the past. One way this is done in many radioactive dating techniques is to use an isochron. However, a recent paper by Dr. Robert B. Hayes has pointed out a problem with isochrons that has, until now, not been considered.
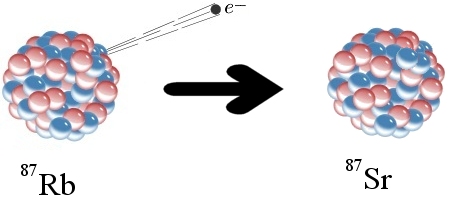
To understand the problem, let’s start with an example of how radioactive dating works. The elements rubidium and strontium are found in many rocks. One form of rubidium (Rb-87) is radioactive. As illustrated above, a neutron in a Rb-87 atom can eject an electron (often called a beta particle), which has a negative charge. Since a neutron has no charge, it must become positively charged after emitting an electron. In fact, it becomes a proton. This changes the chemical identity of the atom. It is no longer Rb-87; it is strontium-87 (Sr-87). Sr-87 is not radioactive, so the change is permanent.
We know how long it takes Rb-87 to turn into Sr-87, so in principle, if we analyze the amount of Rb-87 and Sr-87 in a rock, we should be able to tell how long the decay has been occurring. Of course, there are all sorts of uncertainties involved. How much Sr-87 was in the rock when it first formed? Was Rb-87 or Sr-87 added to the rock by some unknown process? Was one of them removed from the rock by some unknown process?
The isochron is supposed to take care of such issues. Essentially, rather than looking at the amounts of Rb-87 and Sr-87, we look at their ratios compared to Sr-86. The ratio of Sr-87 to Sr-86 is graphed versus the ratio of Rb-87 to Sr-86 for several different parts of the rock. How does that help? Sr-86 is another stable form of strontium, but it isn’t produced by radioactive decay. Thus, it provides an independent analysis of the rock that does not depend on the radioactive decay that is being studied.
The amount of Sr-87 that was already in the rock when it formed, for example, should be proportional to the amount of Sr-86 that is currently there. Since the data are divided by the amount of Sr-86, the initial amount of Sr-87 is cancelled out in the analysis. If some process brought Sr-87 into the rock, it probably brought different amounts of the atom into different parts of the rock, so the ratio of Sr-87 to Sr-86 won’t stay consistent from one part of the rock to another. If a consistent isochron is generated, however, we can be “certain” that no process interfered with the relative amounts of Rb-87 and Sr-87, so the radioactive date is a good one.
Here’s where Dr. Hayes’s paper comes in. He says that there is one process that has been overlooked in all these isochron analyses: diffusion. Atoms and molecules naturally move around, and they do so in such as way as to even out their concentrations. A helium balloon, for example, will deflate over time, because the helium atoms diffuse through the balloon and into the surrounding air. Well, diffusion depends on the mass of the thing that is diffusing. Sr-86 diffuses more quickly than Sr-87, and that has never been taken into account when isochrons are analyzed.
No problem. Now that Dr. Hayes has brought it up, we can take it into account, right? Perhaps, but it’s rather tricky, because the rate of diffusion depends on the specific chemical and physical environment of each individual rock. If the effects of diffusion can be taken into account, it will require an elaborate model that will most certainly require elaborate assumptions. Dr. Hayes suggests a couple of other approaches that might work, but its not clear how well.
So what does this mean? If you believe the earth is very old, then most likely, all of the radioactive dates based on isochrons are probably overestimates. How bad are the overestimates? I have no idea, and I don’t think anyone else does, either. Dr. Hayes’s model indicates it could add as much as 29 billion years to ages determined with rubidium and strontium, although his model is rather simplistic. Most likely, the effect will be dependent on the age. I would think that the older the sample, the larger the overestimate. However, it’s important to note that some radioactive dates (like those that come from carbon-14) don’t use the isochron method, so they aren’t affected by this particular flaw.
As a young-earth creationist, I look at this issue in a different way. As I have stated previously, we just don’t know a lot about radioactive decay. Certainly not enough to justify the incredibly unscientific extrapolation necessary in an old-earth framework. This newly-pointed-out flaw in the isochron method is a stark reminder of that. A good isochron was supposed to be rock-solid evidence (pun intended) that the radioactive date is reliable. We now know that it is not.
I suspect that this flaw is not the last one that will be uncovered.

Dr. Wile, I was waiting for you to comment on this, because I wanted to ask if you think this problem can be extrapolated to other isotopes such as lead and argon. If so, it seems to be a pretty big deal.
It is the standard technique in most radioactive dating methods, including the uranium/lead method and the potassium/argon method. Indeed, the Zaire diamonds I mentioned were dated with the potassium/argon method, and it used the isochron method. As I said, carbon-14 dating is an exception, but most other modern radiometric dates are produced using an isochron.
Dr Wile, I have read Christian old earth perspectives on this that basically acknowledge the variation between the different radiometric dating methods but they all tend to point in the direction of just being “wicked old”. Whether a rock shows a potassium/argon of 2.5 – 4 billion, and the same rock has a uranium/lead 1.5-3 billion, they are both well beyond a mere 6,000 years even though they can differ significantly from one another.
Are the samples we see in the RATE study, for example, just anomalies, existing on the ends of the bell curve, or are these indicative of an endemic misunderstanding of the process? Are there any theories that could account for the accelerated decay rate or how the daughters could have gotten in to the samples?
I agree that most radioactive dates seem to indicate that things are “wicked old,” but then again, you would expect them to. After all, they are mostly dealing with isotopes that have “wicked long” half lives. Thus, any significant amount of daughter product will produce a very old date. In my view, if two different dating schemes give significantly different answers, then either one of them is wrong or both of them are wrong. I am not sure how scientific it is to say, “Well, both of them give an old age, so even if one (or both) of them is wrong, it’s still really old.” It’s possible that both of them are wrong and the object could be very young.
From my experience, discordant dates aren’t uncommon. Unfortunately, many of them don’t get published. That’s not because they are being “hidden.” It’s because they are being excluded. Scientists exclude what we think are anomalous data all the time. Unfortunately, that discarded data might be what gives us real insight.
There aren’t any complete theories that can explain these data…on either side. Young-earth creationists have a hard time explaining the general results of long-lived isotopes and their daughter products being present. Sure, there are reasons to think that half-lives aren’t constant, but then again, if they were fast enough in the past to explain most of the data we see today in a young-earth framework, there is an enormous heat problem. On the other side, old-earthers have a hard time explaining all the discordance. If radioactive dating is so reliable, why do different methods yield different results? Why are some of those differences really, really large?
As is often the case, there are problems on both sides. The side you end up coming down on often depends on which problems you are most comfortable trying to deal with.
You mention “an enormous heat problem”, and this reminds me again of dark matter detection experiments, which try to detect the interaction of dark matter with heavy nuclei. Physicists already theorize that dark matter would affect nuclear decay rates; what if the leftover energy went to the dark matter? This isn’t my field, and I don’t know what the average kinetic energy of the galactic dark matter flows is supposed to be, but I do know dark matter is supposed to be “cold”.
That’s an interesting thought, Jake, but I am not sure it works. The heat problem occurs everywhere there are radioactive isotopes, so throughout the crust and mantle of the earth, for example. The dark matter would have to be there in order to take the heat. Of course, the problem with that is it would throw off the mass of the earth, which would probably affect the moon’s orbit and other things that I haven’t thought of.
Dark matter is called “cold” because it isn’t emitting light. Thus, it is thought to have little excess energy, and it is thought that light doesn’t interact well with it. It doesn’t really mean that dark matter could be a heat sink.
You can think of dark matter here as a lot like the luminiferous ether: physicists actually picture it as part of giant galactic flows – so that the right scale for the size of a flow would be on the order of light-years. Since its interaction with normal matter is incredibly weak, it can very easily pass through the earth. I haven’t thought about how the earth’s gravitational well affects the dark matter, but I can tell you that the picture I gave above comes from the people who do dark matter for a living, so I imagine the fact that the earth would collect dark matter doesn’t cause any problems that conflict with what we know from observing gravitational interactions in the solar system.
And dark matter is classified as “cold” or “hot” based on its speed relative to the speed of light; this is important for cosmological models, because the speed of dark matter is related to the size of structures formed in the early universe. Or something. I’d provide you with links/papers, but I only know what I heard at the seminars about dark matter I’ve attended (there are so many at my university that my friends and I joke about them).
Whether or not heat would be transferred to the dark matter depends on the kinematics of the interaction between dark matter and nuclei, and that I’d have to work out. (Not to mention that different models of dark matter would lead to different interactions.)
Further, I don’t think that the earth, the moon, and such collecting dark matter is that much of a problem: if it’s always been there, we wouldn’t notice it. Are we able to calculate the mass of the earth from our knowledge of its contents, and not just the gravitational force we detect? If we could that’d actually be a way to detect dark matter (if there’s enough of it); so I imagine that we don’t know enough about the density of the earth to do that calculation.
I think if there were much dark matter in the earth, it would be noticeable. After all, we get the mass of the earth from the moon’s orbit, but then we have a good knowledge of the density of the various layers in the earth by studying sound waves that travel through the earth. We also know the overall composition of the crust and mantle from samples. Thus, the only real unknown is the composition of the core. Using the mass and all those other measurements, we deduce that the core is mostly iron with some nickel. It seems to me that if there were a lot of dark matter, that would throw off the calculation, causing us to deduce that the core is made of something much more dense, which wouldn’t be physically realistic. However, I can’t say I am certain about that.
I didn’t realize those were the meanings of “cold” and “hot” when it comes to dark matter. That’s interesting.
I fear it is more a matter of philosophy rather than hard science: to posit gradual change in fossil record is only itself possible if the phyla being examined is similar in appearance, but apparently better adapted to its environment than earlier assumed examples.
The problem with that, is that, in the first case, there appear to be no transitional fossils when there should be millions , and to make the assumption previously herein stated, evolutionary conclusions are more akin to a combination of wishful thinking combined with a sympathetic magic mindset, than to observable examples.
When we are our own “gods”, we have made no room for the possibility of another.
So, intelligent design is discarded, in favour of e redefinition of the word, “Theory”. Evolution is taught as established fact, and scientific enquiry is severely trammelled by those who prefer a status quo.
Every fossil between organisms alive now and abiogenesis is a transitional fossil, Tony.
There are also transitional fossils and organisms in the misguided definition of the word you are using
I admire your faith, Cromwell. There isn’t even a viable mechanism for abiogenesis, much less any evidence that it occurred. Yet you state it as fact. Then, you claim that all fossils are a transition between that unrealistic event and the life we see now. That’s the stuff of faith to one who must believe in such things, but it is a level of faith that I cannot muster!
Jay,
Thanks for writing an informative article. I haven’t wandered over to the nearby college library to look at the original article. Error bars have their place, but you are correct in pointing out that they are often misunderstood not only by the general public, but by scientists who are not savvy in radiometric dating.
I would have worded this sentence differently: “If a consistent isochron is generated, however, we can be ‘certain’ that no process interfered with the relative amounts of Rb-87 and Sr-87, so the radioactive date is a good one.” I would replace “be certain” with “have a high level of confidence,” because most geochronologists know there are processes that may produce false isochrons.
I am not convinced that differential diffusion of isotopes will be all that significant. After all, fractionation of light elements, such as oxygen, provides us with all sorts of insights into geologic processes because the mass difference between O-16 and O-18 is rather significant, whereas the mass difference between Sr-86 and Sr-87 is not all that great, in terms of ratios. The differences are even less significant for more massive isotopes such as in samarium-neodymium dating (Nd-143 and Nd-144).
If fractionation does turn out to be important for isochrons, one would expect that there would be a trend, with lighter nuclides (e.g. Rb-Sr) being more affected than heavier nuclides (e.g. Sm-Nd). I am also wondering if Dr. Hays addressed how isotope fractionation would affect U-series concordia diagrams. As it is, there is a general correlation of dates obtained by radiometric dating from the top to the bottom of the geologic column. Strongly discordant dates happen (and young-Earth creationists focus on these), but roughly concordant dates are common; otherwise geologists would not trust the methods. It seems strange, if diffusion is a problem, that nuclides with very different masses are effected in the same way.
My arguments do not mean that fractionation shouldn’t be considered in isochron dating. Again, I admit I haven’t read Dr. Hayes’s article. But I’m wondering if isotope fractionation really is going to be all that significant.
Let’s say this turns out to be huge; that this differential diffusion makes a big difference in radiometric dates. Perhaps Earth is only 3.5 billion years old instead of approximately 4.6 billion years old. (This would require similar diffusion rates in cold meteorites as in warm crustal zircons). This would be very interesting, and would cause geologists to have to re-write many books, but the general story of geology would stand. This is because geologists do not believe Earth is billions of years old because of radiometric dating. Radiometric tools merely give us firm pegs to hang our signs on for the various eras, periods, and epochs of Earth history.
Thanks for your comment, Kevin. I would have to disagree with your suggested change in wording, however. While most (definitely not all) geochronologists do understand that there are false isochrons, that is never the way it is presented to students or the general public. Isochrons are routinely presented as “proof positive” that the radioactive date is reliable. This is unfortunate, of course, but it seems to be the norm when propaganda replaces science.
If you aren’t convinced that differential diffusion is a problem, you need to read the article. Hayes shows how diffusion alone can produce what looks like an isochron in the Rb/Sr system. I think what you are missing is the chemistry involved. When we are dealing with trace elements (not substances that are part of the crystal lattice), differential diffusion can have a significant effect. It is also not clear that there would be a general trend like you suggest. Diffusion also depends on chemical issues. When you are dealing with different elements, you are dealing with completely different diffusion scenarios.
I don’t recall Dr. Hayes discussing uranium-series dating. Unfortunately, I am currently in Canada and cannot use my university’s system to access the article. I do remember that his model is only for the Rb/Sr series to show the reality (and significance) of the effect. Since concordia diagrams also involve isotope ratios, however, I suspect that this problem exists there as well.
I will have to disagree with you that “concordant dates are common.” In my experience, discordant dates are common. In fact, they might even be the majority. However, most discordant dates aren’t published. As a result, we really don’t know. As I told Tim, this isn’t because data are being “hidden.” It’s just that scientists tend to exclude discordant dates as “noise” when, in fact, they might be much more than that.
I have no doubt that those who want to believe in an old earth will be able figure out a way to keep the overall story of geology the same, regardless of how important this effect turns out to be, if that can even be determined to any reasonable precision. However, I do suggest a change in wording to your statement, “This is because geologists do not believe Earth is billions of years old because of radiometric dating.” You should put “most” in front of “geologists,” as I have spoken to one Ph.D. geologist who says she would be a young-earth geologist if it weren’t for radiometric dating. Yes, there are other issues at play (as is the case with any over-arching scientific idea), but to her, radiometric dating is the most important reason she believes in an old earth. I have no idea whether she is the norm or the exception, but she does exist.
Oh – they’re not part of the crystal lattice. I was wondering how diffusion made any sense…
I’d have to count myself as one geologist who was initially held back from accepting the young earth model by radiometric dating. When I started my journey from old earth-evolutionism, it was much easier to see the flaws in evolutionary theory than those in the old age model. That was back before the Web–it wasn’t until I’d subscribed to the Creation Research Society Journal for a couple of years that I read enough to convince me that radiometric dating had some significant assumptions that warranted more skepticism about their reliability for age dating.
Other than radiometric dating, I didn’t see any significant geologic datasets that pointed unequivocally to an old earth, and there were a lot that fit much more easily into the young earth model, especially when combined with the concept of a catastrophic global flood.
Thanks for your personal story, SJ. I guess that makes at least two geologists for whom radioactive dating was a big factor in their belief in an old earth. I am glad that you eventually saw the problems associated with that.
Rubidium readily substitutes for potassium in the crystal lattice of minerals, and strontium readily substitutes for calcium. Rb and Sr are still considered to be trace elements, even when incorporated into the lattice. When Rb-87 decays to Sr-87, the resulting strontium ion is chemically out of place in the lattice structure.
Dr Wiles,
Thanks for your response. I don’t know if you have heard of the Japanese company that wants to be the first to drill into earth’s mantle, but it seems like that could be a very interesting litmus test for radiometric dating. From my understanding, the “stopwatch” for these isotopes starts when the magma cools on the surface, is that right? What might we find if we can dip into the magma and test it immediately? Seems like that might be a good calibration for these radioisotopes.
Many radioactive dating systems start with an assumption about what happens at the point of solidification. So, for example, the potassium/argon system assumes that all argon has “bubbled off” the lava, so when the rock is first formed, there is no argon in the system at all. Thus, any argon in the rock must have come from radioactive decay.
To some extent, those assumptions have been tested already by “dating” igneous rock that is known to be only hundreds of years old, because the lava flow was recorded historically. In all cases, there is a lot of argon in the rock, indicating that the assumption is false. Now, of course, proponents of the potassium/argon method say the amount is small, so when you are dating something that is “hundreds of millions” of years old, it adds just a small error to the date. Of course, that’s assuming that the amount of argon in the atmosphere, mantle, etc. was the same “hundreds of millions” of years ago.
I am not sure what directly testing mantle magma will tell us about radioactive dating, because lots of things happen to the lava as it is flowing over the surface of the earth. Obviously, directly sampling mantle magma will tell us a lot, but I am not sure if it will tell us anything about radioactive dating.
The samples from the mantle would not be magma, but solid rock. The mantle is almost entirely solid.
We already have samples of the mantle, in the form of inclusions (e.g. diamond) in mantle-derived volcanic rocks, and in the form of deep slices of oceanic lithosphere called ophiolites that have been scraped off of oceanic plates as they subduct beneath continents. Ophiolites have, in general, been altered from their original form, so pieces of raw, unaltered mantle rock would make for a number of interesting studies.
Actually, we call the rock in the mantle ‘plastic rock,’ because it is not exactly solid or liquid. It is a bit in between.