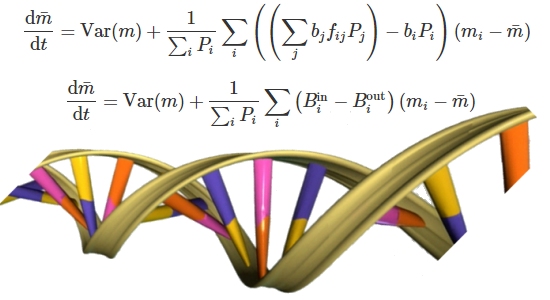
In 1930, Dr. Ronald Fisher (statistician and geneticist) wrote a book entitled, The Genetical Theory of Natural Selection. In that book, he produced a mathematical proof of what he called the “Fundamental Theorem of Natural Selection.” Partly due to his difficult writing style and partly due to a feud in the literature with American geneticist Dr. Sewall Wright, his theorem was misunderstood for quite some time. In 1972, however, physical chemist Dr. George R. Price explained it in a detailed way and showed that it was mathematically correct.
What is the importance of the Theorem and what does it say? This quote from Essential Readings in Evolutionary Biology (by Francisco J. Ayala, John C. Avise, 2014) answers both of those questions:
…Fisher’s formulation of the “fundamental theorem of natural selection,” which would play a preeminent role in the future development of evolutionary genetics: “The rate of increase in fitness of any organism at any time is equal to its genetic variation in fitness at that time.” (p. 73)
In other words, natural selection will cause an organism to increase in fitness as long as its population has variation in the genes associated with fitness. The more variation in those genes, the faster the organism will increase in fitness. As Drs. Ayala and Avise indicate, this theorem became very important in shaping the field of evolutionary genetics.
While Fisher’s fundamental theorem is still quite correct, it is limited. In particular, it doesn’t take the effect of mutations into account. However, there is a corollary attached to the theorem: Since mutations should increase the genetic variation in a population, mutations should lead to a faster rate of fitness increase. While that corollary was important in shaping Neo-Darwinism, a recent paper published in the Journal of Mathematical Biology has shown that it is false when even mildly realistic conditions are considered.
The paper was written by Dr. William F. Basener, Emeritus Associate Professor of Mathematics and Statistics at the Rochester Institute of Technology, and world-renowned geneticist, Dr. John Sanford. I know that Dr. Sanford is a young-earth creationist. I don’t know about Dr. Basener. He is definitely associated with the intelligent design movement, however.
In their paper, Basener and Sanford develop a mathematical model based on Fisher’s original work. They show that when mutations are not considered, their model is equivalent to Fisher’s theorem. Then they add mutations to the model. They show that if there are just as many beneficial mutations as harmful ones, the results are consistent with the corollary that is attached to Fisher’s theorem. However, as everyone knows, that is an unrealistic view of mutations. There are far more harmful mutations than beneficial ones.
They then survey the literature, looking for the proper ratio of harmful mutations to beneficial ones. According to their search, the best number they could find (from an evolutionary standpoint) is that there are a million harmful mutations for each beneficial one. They decide to be generous, saying in their model that there is a beneficial mutation for every 1,000 harmful ones. Using this (incredibly generous) value, here is what they show:
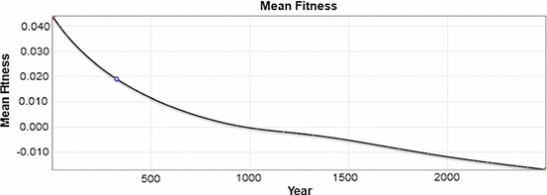
So when a moderately realistic view of mutations (that is still incredibly generous to the evolutionary hypothesis) is used, we see that an organism’s fitness doesn’t not increase over time. In fact, it decreases rather rapidly. Thus, the corollary to Fisher’s theorem is falsified under even moderately-realistic conditions.
Now please understand that Fisher’s theorem is not used very much these days. I had never heard of it, and I asked two biology professors I know (both are evolutionists) if they had heard of it. Neither of them had. Thus, I don’t think the fact that Fisher’s corollary has been falsified is a big deal to modern evolutionary science. However, I do think it mathematically verifies what creationists and intelligent design advocates have said for a long time: the kinds of mutations that actually happen in nature don’t generally lead to an increase in fitness, especially when populations are considered.

How would this work when applied to Gould’s ideas of P.E. ? I’m probably oversimplifying it, but he seems to suggest “special” times in evolutionary history where the mutation rates & averages are different than what we study today. Almost like catastrophic geology theory applied to biology, no?
Could someone pushing Punctuated Equilibrium (or have they) posed an apparatus for this? I’ve heard “more radiation” thrown around but wouldn’t the above study suggest that in addition to just adding more mutations, some sort of “comb” would need to be present. I’m not speaking of natural selection, but a filter that somehow screens out bad mutations in real time as they occur. I guess for this to happen the genome would have to understand the overall organism blueprints and somehow guess if mutations would add or detract or be of use in future.
Both Fisher’s theorem and this model assume that evolutionary changes are small, so neither one of them applies directly to punctuated equilibrium. However, as you suggest, this study would indicate it is even worse for punctuated equilibrium, because the mutation rate is supposed to be much higher in punctuated equilibrium. Thus, unless there is some way you could argue that in high-mutation times, the ratio of harmful mutations to beneficial ones decreases significantly, this model would say that the fitness declines even more rapidly.