Was mathematics discovered or invented? That might seem like an odd question, but it is an important one. I haven’t seen any official poll on the matter, but I suspect that most mathematicians, philosophers, and scientists would say that it must have been invented. After all, math is a tool. We use it for accounting, parceling out land, etc. Surely people invented this tool and then improved on it over time. If that’s really true, however, there is a deep mystery that is awfully hard to explain. Nobel laureate Dr. Eugene Wigner (a theoretical physicist and mathematician) put it this way:
The first point is that the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and that there is no rational explanation for it.
Think about it. We didn’t invent the natural world. We simply study it. If we invented mathematics, why does it play such an integral role in our understanding of the natural world?
In my opinion, there is no mystery as to why mathematics is so useful in the natural sciences. That’s because I don’t think we invented it; I think we discovered it. Indeed, I think it is the language of creation. As Galileo wrote:
[The universe] cannot be read until we have learnt the language and become familiar with the characters in which it is written. It is written in mathematical language, and the letters are triangles, circles and other geometrical figures, without which means it is humanly impossible to comprehend a single word.
I was reminded of Galileo’s wise words when I read a short paper by two professors from my alma mater, the University of Rochester.
The paper discusses using a quantum mechanical technique known as variational computation to determine the energy levels in an atom. The quantum mechanical model is (so far) the most accurate model of the atom. However, the mathematics are very complex. As a result, the equations cannot be solved in an exact manner for most atoms. That’s where variational computation comes in. It allows you to approximate the solutions for the equations so that you can apply the quantum mechanical model to any atom. The more approximations you make with variational computation, the more precise your solutions become.
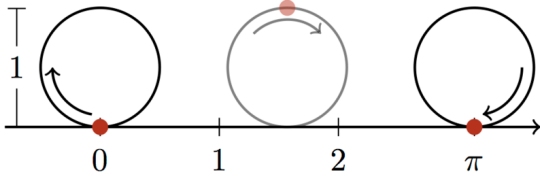
In mathematics, there are also things that must be approximated. One of them is the value for pi, the ratio of the distance around a circle to the diameter of that circle. The drawing at the top of this post gives you a way to visualize what pi means. If a wheel has a diameter of 1 meter, it will travel a distance of pi meters when it makes one complete rotation without slipping. It turns out that the value of pi cannot be calculated in an exact manner. Instead, its value must be approximated. If you do a few approximations, you get 3.14. If you do a few more, you get 3.1416. If you do a few more, you get 3.14159. The more approximations you do, the more accurate decimal places you will get, and therefore, the more precise your value for pi will become. However, you will never get an exact value for pi, because there isn’t one. The decimal places go on forever. Because of that, pi is called an irrational number.
How does this relate to the paper I am discussing? Well, the authors decided to apply variational computation to a system that doesn’t require it: the hydrogen atom. This atom is simple enough that the equations of the quantum mechanical model can be solved exactly, so there is no need to approximate their solutions. Nevertheless, the authors decided to approximate the solutions anyway. When they did, they noticed something. Their solution ended up containing an equation that had been developed by a natural philosopher named John Wallis back in 1655, more than 200 years before quantum mechanics was proposed!
Back then, Wallis developed one of the means by which mathematicians can approximate the value of pi. It turns out that this same approximation simply “falls out” of quantum mechanics when variational computation is applied to the hydrogen atom. In other words, the physics of the hydrogen atom contains one of the means by which we determine pi! As the authors state:
The existence of such a derivation indicates that there are striking connections between well-established physics and pure mathematics that are remarkably beautiful yet still to be discovered.
Indeed. Modern science is still demonstrating the truth of what Galileo wrote nearly 400 years ago.

Thanks for sharing this, as a physics grad student this certainly perked my attention.
I think we have to be very careful anytime we claim math and science are exactly similar. Math allows proofs; science doesn’t. The equation the authors use for the hydrogen atom technically isn’t correct (not relativistic and no electron term). In fact, it is itself only a mathematical approximation of a more accurate mathematical equation, thus, it has no true physical meaning and is just a plain old differential equation — nothing more.
When in math land, series’ pop up all of the time when solving differential equations. Math functions like “sin(x)” can be written as a series of numbers which can come from derivatives (the factorial part) and other mathematical operations.
Having said that, I do agree with what you said: math was discovered. Here’s some examples that come to mind where math seems to perfectly fit with what we see.
1. Spheres. The universe is made of spheres. If you look at the most fundamental particles, for example the electron, our best experimental evidence suggests that they are dimensionless, point like particles which produce a perfectly spherical and symmetric probabilistic wave function.
2. Special relativity. We assume that space is flat in special relativity, when objects move at speeds close to the speed of light they flatten, linearly, perfectly linearly (as far as we can tell experimentally, actually, general relativity contradicts this, but in order to see the curvature you need HUGE, massive bodies).
That’s the only two that came to mind. Anyway, thanks for posting. By the way, i read almost all of your posts; i’m a big fan! I’m always surprised at how well you seem to understand the wide range of topics that you post. Keep it up!
I never claimed math and science are exactly similar, Seth. I merely claimed that math is fundamental to science specifically because it is the language in which Creation was written. I do agree with you that science cannot offer proof, while math certainly can. I also agree that infinite series crop up all the time in both science and math. However, those infinite series are (almost) infinite in variety. Thus, the fact that the infinite series for pi shows up in the variational computation of the hydrogen atom is important, as the quote from the article makes plain.
Interesting thread. I don’t like math but I see this subject come up a lot.
I think it shows creation also. Yet I would spin that, as the bible says, God has measured the universe out.So math is a language of this measurement. I suspect its not the actual measurement however. Its a special case amongst the true measurement.
Man didn’t invent it but simply discovers it works. Yet still wrong to say its reality I think.just a special case.
It surely demands that the creator of a ordered universe was a thinking being.
How else could measurement and math organize itself??
Yes, math was always there to be discovered. Furthermore, math and science knowledge don’t always progress in a forward direction. I think ancient civilizations (including pre-flood inhabitants) could have discovered things like the Pythagorean Theorem before the Greeks did.
This is a fascinating article. Thanks!
It appears that God also loved to employ the Fibonacci sequence in the creation.