July 2018 : Proslogion

Mathematics Leads Biologists to Discover a New Cell Shape!

In 1619, Orazio Grassi (a mathematician, astronomer and architect) wrote about three comets that had recently appeared in the sky. He gave evidence that they must have been far from the earth, even beyond the moon. Galileo wrongly believed that comets were in earth’s atmosphere, and so he wrote Il Saggiatore (The Assayer) in reply. Although Galileo’s overall argument was wrong, the piece does contain a statement that is quite profound:

Philosophy [he is referring to what we call “science” today] is written in this grand book, the universe, which stands continually open to our gaze. But the book cannot be understood unless one first learns to comprehend the language and read the letters in which it is composed. It is written in the language of mathematics, and its characters are triangles, circles and other geometric figures without which it is humanly impossible to understand a single word of it; without these, one wanders about in a dark labyrinth.

While most scientists who use this quote are talking about physics and perhaps chemistry, the fact is that mathematics seems to be the language in which God wrote His creation. As a result, all areas of science (even biology) require the use of mathematics to unlock the true secrets of creation. I recently ran across a paper that illustrates this point rather well.

The authors were using a mathematical technique called Voronoi Diagramming to model how certain cells in an embryo pack together to form the shapes of the organs that are developing. Generally speaking, most biologists assume that the cells become column- or bottle-like in shape so that they can squeeze together and form the smooth curves that characterize the shapes of the organs. However, their mathematical model predicted that another set of shapes would develop – shapes that are so unique they don’t even have a name. As a result, the authors call the shapes scutoids, which refers to the scutum and scutellum, features found on certain insects, like beetles.

A rose chaffer beetle (click for credit)

Drawings of two scutoid-shaped cells are shown on the left side of the illustration below, and the way those two shapes fit together are shown on the right side of the illustration.

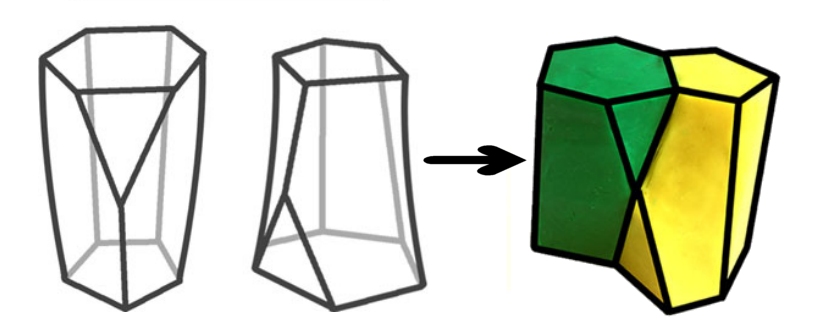
The two drawings on the left represent scutoid-shaped cells. The colored drawing on the right shows how they fit together. (images from the paper being discussed)

Now, of course, the authors didn’t just believe the results of their mathematical model. After all, the mathematical model contains assumptions, and those assumptions could be flawed. However, armed with the knowledge of those shapes, they examined specific tissues in developing fruit fly larvae. Sure enough, they found tissue structures that are composed of scutoid-shaped cells.

Why do cells form these shapes in developing fruit fly embryos (and presumably other embryos)? The authors state:

Using biophysical arguments, we propose that scutoids make possible the minimization of the tissue energy and stabilize three-dimensional packing. Hence, we conclude that scutoids are one of nature’s solutions to achieve epithelial bending.

In other words, they produce the most stable tissue at the lowest energy.

Now remember, the reason the authors found this brand-new cell shape is because they started with mathematics, just as Galileo instructed. Writing more than 300 years after Galileo, Sir James Hopwood Jeans (English physicist, astronomer and mathematician) tells us why he thinks Galileo was right:

Lapsing back again into the crudely anthropomorphic language we have already used, we may say that we have already considered with disfavour the possibility of the universe having been planned by a biologist or an engineer; from the intrinsic evidence of his creation, the Great Architect of the Universe now begins to appear as a pure mathematician. [The Mysterious Universe, Cambridge University Press 1931, p. 122]

This Could Be One of the Most Important Scientific Papers of the Decade

What best explains the common features shared by animals? According to this study, it’s the fact that they are designed.

More than eight years ago (have I really been blogging that long?), I was excited to see the appearance of a new peer-reviewed journal, BIO-Complexity. I thought it was going to have a lot of impact on the science of biology, but so far, its impact has been minimal. A few good studies (like this one and this one) have been published in it, but overall, it has not published the ground-breaking research I had hoped it would.

That might have changed. I just devoured the most recent study published in the journal, and I have to say, it is both innovative and impressive. It represents truly original thinking in the field of biology, and if further research confirms the results of the paper, we might very well be on the precipice of an important advancement in the field of biological taxonomy (the science of classifying living organisms).

The paper starts by detailing the fact that while evolutionists have always hoped that living organisms can be organized into a tree of life (starting with one universal common ancestor and branching into all known organisms), that hope has never been realized. In particular, when we look at organisms on the genetic level, no consistent tree can be produced. Instead, a “tree-like” arrangement can be made, but it needs all sorts of rescuing devices to explain the many inconsistencies that crop up.

Nevertheless, the fact that the structure somewhat resembles a tree tells us something. It tells us that the organisms we see today contain a lot of commonalities. However, since no consistent tree can be constructed, it is doubtful that those commonalities are the result of evolution. How, then, can scientists understand the “tree-like” structure of biological relationships?

The author of this new paper, Dr. Winston Ewert, makes a suggestion that is both innovative and, at the same time, so obvious it makes me wonder why I haven’t heard it before.

Continue reading “This Could Be One of the Most Important Scientific Papers of the Decade”

Coming “Soon”: Science in the Atomic Age

My elementary science series is finished, and I am currently working on a junior-high course that carries on with the theme of teaching science through history.

My elementary science series has been complete for a while now, and I am thrilled to see it becoming popular in the homeschooling community. The series teaches students science in roughly chronological order. It begins with the days of creation (Science in the Beginning). It then moves on to the ancient Greeks (Science in the Ancient World), teaching science in the order it was learned. It continues through roughly the end of the 1800s (Science in the Industrial Age). If a student completes all five books in the series, he or she will be very well prepared to start learning science in a detailed way in junior high school.

For quite some time, I have been hearing from homeschooling parents who would like me to continue the theme of teaching science through history into the junior high school years. With the encouragement of my publisher, I have decided to give it a try. I am currently working on Science in the Atomic Age. It will be a junior-high-school level course that covers many of the scientific discoveries made in the 20th and early 21st centuries. I plan to discuss the modern view of the atom, how atoms join together to make molecules, what the molecule known as DNA does, the cell as the basic building block of life, several of the advances that have been made in medicine, the structure and characteristics of the universe as a whole, radioactivity, and nuclear reactions.

While it carries the theme of teaching science through history, there will be at least four important differences between this course and my elementary courses. First, in the elementary course, I teach all of science on a timeline. As a result, the books change science topics constantly. In the first 15 lessons of Science in the Ancient World, for example, students start by learning the importance of math in science, then learn about the science of music, then learn about atoms, and then learn about medicine. It’s difficult to cover scientific advancements made in the 20th and 21st centuries that way, because the issues become more complex, and it is important to see the development of one particular topic over the years. So while I will still discuss science in the context of history, it will be by topic.

In other words, when I write about our modern understanding of the atom, I summarize what was known towards the end of the 1800s. I then step students through the history of atomic science, eventually ending with our current understanding of the atom. As a result, students see how the entire field of atomic science developed through the course of the 20th and 21st centuries. I then move on to molecules, but once again, I step back to the end of the 1800s and discuss the history of how our understanding of molecules developed. When I get to DNA, I “reset the clock” once again, starting with what was known at the end of the 1800s and working forward to the present day.

Now, of course, the focus is on the science, not the history. The students aren’t learning what happened in the world during the 20th and 21st centuries, unless those events affected scientific progress (like the World Wars). Instead, they learn the history of how scientists were led to our modern views. Because of this approach, students not only learn the science of what is being discussed, but they also learn the scientific reasoning used to reach our current understanding of scientific issues.

The second major difference between Science in the Atomic Age and the other books in my series is that it will be much longer. More science has to be covered in junior high school, so unlike my elementary books, this book is designed to be used every day. The third major difference is the frequency of experiments. In my elementary series, each time the student does science, he or she has a hands-on activity, usually an experiment. While there are still experiments and hands-on activities in this book, there aren’t as many. In a two-week period, students will do three or four experiments or activities. That means the student will be expected to do more reading in this course.

The final major difference is that the book switches from a notebooking approach when it comes to reviewing the material to a question/answer approach. There are “comprehension check” questions the student needs to answer while he or she is reading. Then, at the end of each chapter, there is a chapter review to help the student remember everything that was learned. Finally, there is a test for every chapter. In order to prepare the student for high school and beyond, it is important that the student answers all of those questions and takes the test.

I have only just begun writing this course, so it won’t be available for this academic year. However, I hope to be able to choose a group of students to “field-test” the book for the 2019-2020 academic year. However, that will depend on my progress. Assuming that I can start the “field-testing” on time, the book should be ready for general use in the 2020-2021 academic year. Of course, the Lord might have quite different plans, so stay tuned to find out what happens!

No, We Won’t Have Dinosaurs in Two Years!

Even with a LOT of tinkering during embryonic development, only minor changes could be made in a chick’s skull.
(image from Bhullar et. al. article linked below)

A little while ago, I wrote an article about how silly “science journalism” can get. The article was about the popular media’s claim that scientists were about to bring mammoths back from extinction. I explained how the idea was based on real research, but the goal of the research was not to bring mammoths back from extinction. In addition, if anything concrete comes from the work, it will probably be decades from now. In response to that, a student sent me an even sillier article, which comes from that bastion of journalistic integrity, People. It states the following:

Famed paleontologist Dr. Jack Horner, who’s been a consultant on all four films and is the real-life inspiration for Jurassic Park’s dinosaur expert Dr. Alan Grant, believes we’re (optimistically) just five years away from genetically engineering a dinosaur.

This article was written back in 2015, so based on Dr. Horner’s optimistic projection, we should be just two years away from having dinosaurs roaming around in some laboratory.

So what is the source of Dr. Horner’s optimism? He thinks that birds evolved from dinosaurs, so he thinks that we could genetically “turn back the clock” and transform a bird into a dinosaur. He claims that this has already been done to some extent:

In what Horner calls a definitive “proof of concept,” a group at Harvard and Yale “just recently, within the last few weeks, were able to transform the head of a bird back to actually reverse-engineer the bird’s snout back into a dinosaur-like snout.”

There are so many things wrong with that statement, it is hard to know where to start. However, I will give it a try.

Continue reading “No, We Won’t Have Dinosaurs in Two Years!”

“Nylon”-Digesting Bacteria are Almost Certainly Not a Modern Strain

This marine bacterium has the ability to digest nylon waste products, despite the fact that it doesn’t live in an environment that contains nylon waste products. (click for credit)

Evolutionists are fond of stating “facts” that aren’t anywhere near factual. For example, when I was at university, I was taught, as fact, that bacteria evolved the genes needed to resist antibiotics after modern antibiotics were made. As with most evolutionary “facts,” this turned out to be nothing more than wishful thinking on the part of evolutionists. We now know that the genes needed for antibiotic resistance existed in the Middle Ages and back when mammoths roamed the earth. They have even been found in bacteria that have never been exposed to animals, much less any human-made materials.

Of course, being shown to be dead wrong doesn’t produce any caution among evolutionists when it comes to proclaiming the “evidence” for evolution. When Dr. Richard Lenski’s Long Term Evolution Experiment (LTEE) produced bacteria that could digest a chemical called “citrate” in the presence of oxygen, it was hailed as definitive “proof” (a word no scientist should ever use) that unique genes can evolve as a result of random mutation and selection. Once again, that “fact” was demonstrated to be wrong in a series of experiments done by intelligent design advocates. They showed that this was actually the result of an adaptive mutation, which is probably a part of the bacterial genome’s design.

Recently, I learned about an impressive genetic study by young-earth creationists Sal Cordova and Dr. John Sanford. It lays waste to another evolutionary “fact” I was taught at university: the recent evolution of nylon-digesting bacteria. The story goes something like this: In 1975, Japanese researchers found some bacteria, which are now charmingly named Arthrobacteria KI72, living in a pond where the waste from a nylon-producing factory was dumped. The researchers found that this strain of bacteria could digest nylon. Well, nylon wasn’t invented until 1935, and there would be no reason whatsoever for a bacterium to be able to digest nylon before it was invented. Thus, in a mere 40 years, a new gene had evolved, allowing the bacteria to digest something they otherwise could not digest.

Of course, we now know that this story isn’t anywhere close to being true.

Continue reading ““Nylon”-Digesting Bacteria are Almost Certainly Not a Modern Strain”

Print Reading versus Digital Reading: Which Produces Better Comprehension?

I saw this Science Alert article come across my Facebook feed a few days ago, and I read it with interest. Written by two researchers from the University of Maryland, it makes some pretty strong statements about the effectiveness of reading a digital article compared to a print article. Essentially, the researchers say that for specific kinds of articles, students’ comprehension is better if the article is read in print form as opposed to digital form. They make this statement based on a review of the studies that already exist as well a study they published two years ago. While I think they are probably correct in their assessment, I am struck by how small the difference really is.

For the purpose of this article, I will concentrate on their new study. In their Science Alert article, they refer to it as three studies, but it is published as a single paper. In the study, they had 90 undergraduate students who were enrolled in human development and educational psychology courses read a total of four articles: two digital and two in print. Two of them were newspaper articles and two were excerpts from books. They were all roughly the same length (about 450 words). They dealt with childhood Autsim, ADHD, Asthma, and Allergies. Presumably, all of those topics would be of interest to the students, given the classes in which they were enrolled.

Before they did any reading, the students were asked to assess themselves on their knowledge of the four topics about which they would be reading. They were also asked which medium they preferred to read: digital or print. They were also asked about how frequently they used each medium. They were then asked to read the articles, but the order in which the articles were read changed from student to student. Some would switch between digital and print, while others would read the first two in one medium and then the second two in the other medium. That way, any effect from switching between the media would not be very strong.

After each reading, students were asked to identify three things: the main idea of the article, its key points, and any other relevant information that they remembered from the article. The researchers had asked the authors of the articles these same questions as well as two independent readers. Those were considered the correct answers. Two trained graders independently compared the students’ answers to the correct answers, and the grades they assigned were in agreement 98.5% of the time. For the 1.5% of the time they didn’t agree, they then discussed the grading and came to a mutual agreement.

After all four readings and tests, the students were then asked in which medium they think they performed best. As you will see, that’s probably the most interesting aspect of the study.

Continue reading “Print Reading versus Digital Reading: Which Produces Better Comprehension?”

Will Scientists Resurrect the Woolly Mammoth?

Model of a woolly mammoth at the Royal BC Museum in Canada. (click for credit)

One of my former students sent me an article from The Telegraph, a news outlet in the UK. The headline reads:

Woolly mammoth will be back from extinction within two years, say Harvard scientists

The article was written in February of 2017, so the student wanted to know if there would really be living woolly mammoths next year. The answer, of course, is absolutely not. This article is just another example of how many “science journalists” understand neither science nor journalism. Nevertheless, the actual scientific story is interesting, even though it isn’t nearly as sensational as what is indicated in The Telegraph‘s article, or articles found on other sites, such as here and here.

These articles are attempting to report on the Woolly Mammoth Revival Project, which is headed by Harvard professor Dr. George Church. As its website indicates, the goal is not to bring back the identical mammoth species again. Instead, its goal is to create some kind of elephant/mammoth hybrid that can live in colder climates. Why would it want to do that? For ecological engineering.

At some time in the past, woolly mammoth herds (and herds of other cold-adapted animals) roamed what are now the evergreen forests in the northern latitudes. This kept the growth of evergreens in check, making those areas more like grasslands. In addition, the mammoth herds would pack down and scrape away snow. Without this “land reshaping,” snow insulates the soil below, reducing the depth to which it freezes. As the deeper soil thaws, it releases greenhouse gases, and the worry is that those released greenhouse gases will accelerate global warming, aka “climate change.” Now please note that actual data indicate thawing soil will reduce greenhouse gases in the atmosphere, but most “climate change” alarmists aren’t interested in the data.

In the end, then, the Woolly Mammoth Revival Project hopes to populate the north with cold-adapted, elephant-like animals that will once again turn the northern evergreen forests into grasslands, packing down and scraping away the snow as they roam.

Continue reading “Will Scientists Resurrect the Woolly Mammoth?”

Death and Transformation

From left to right, Robert Kaufmann, JJ Brannon, yours truly, and John Ashmead.

I have to warn you. This post is different from the normal fare you will find on this site. It represents more of an unfinished thought than an argument or an analysis. However, I want to share this unfinished thought with you, because I can’t help but think that it might be important, at least in some way.

This past weekend, I attended a memorial service and wake for a man who was taken from this earth far too soon: James Jerald (JJ) Brannon. I met JJ at a science fiction convention that I speak at nearly every year. He was the cousin and dear friend of the man who invited me to participate in the conference, and he was also a speaker at the conference. In fact, we did several panel discussions together over the years, such as the one pictured above. That particular panel was about the diseases we might expect to see in the 21st century.

JJ was, in a word, unique. He had many awesome qualities, but he was, quite frankly, incredibly difficult to deal with. He often portrayed himself as an expert on subjects about which he was not well-educated, and unless you worked hard to hold him in check, he would monopolize any conversation he was a part of. He also went on and on and on and on and on when a subject was very important to him.

Now don’t get me wrong. JJ was incredibly difficult to deal with, but he was also an amazing friend. I genuinely enjoyed seeing him, and I was truly fond of him. Also, he loved me and his other friends (and his family) fiercely. However, after spending a lot of time with him, I often found myself getting annoyed with him. His cousin (the friend who introduced us) often felt the same way. One thing he would often complain about is that when JJ called, it was never a short conversation. As I said, JJ could go on and on and on, especially when a subject really interested him.

When I went to his memorial service, I wasn’t quite sure what to expect. What would people say about this wonderful but annoying man?

Continue reading “Death and Transformation”